We already know that factors are two numbers or variables that are multiplied together. To get a product, we multiply factors. Factoring is the process of breaking down a product into its parts.
To factor a whole number like 6, we make a list of every other whole number that divides evenly into 6. The numbers 1, 2, 3, and 6 are all equally divisible by 6.
Every number has itself and 1 as factors, since any number times 1 is that number. Prime numbers are numbers where the only whole factors are 1 and the number itself. Composite numbers are those that have at least one other factor.
PRIME FACTORIZATION
The prime factorization of a number is a multiplication sentence made up of only prime numbers, the product of which is the number. For example, the prime factorization of 6 is (2)(3), because 2 and 3 are both prime numbers, and they multiply to 6.
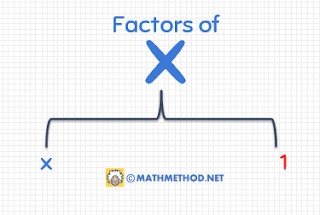
There are variable that has exactly two factors: 1 and itself.
As you can see in the above illustration, number $7$ is a prime number and its only factors are $1$ and $7$. We can say that every variable has exactly two factors: $1$ and itself.
The factors of $x$ are $1$ and $x$. If a term has a coefficient, some of the factors of that term are its coefficient and its variables (with their exponents). That coefficient can be broken down into its factors, and the variables with their exponents can be broken down into their factors.
Let's look at another example.
The term 8x can be factored into $(8)(x)$, because 8x means “$8$ multiplied by $x$.” $8$ can be factored into $(2)(4)$, and $4$ can be factored into $(2)(2)$. The factorization of $8x$ is $(2)(2)(2)(x)$. None of the values in parentheses can be factored any further.
The term $3{x^2}$ can be factored into $(3)(x^2)$. $3$ is a prime number, so it cannot be factored any further, but $x^2$ is equal to $(x)(x)$. $3{x^2} = (3)(x)(x)$.